Monday, June 22, 2009
Hi TianChong here =] Today i am going to talk about the areas of triangles.Ok lets first start off today by asking.. How many formulas do you all know?
Well the most basic ones that any student who studied mathematics up to high school will probably know : Area = 1/2 x base x height
or by using another commonly used method, trigonometry: Area = 1/2 absinC
So now, i am going to talk about some other methods that are not commonly used such as by using coordinates :
If vertex A is located at the origin (0, 0) of a Cartesian coordinate system and the coordinates of the other two vertices are given by B = (xB, yB) and C = (xC, yC), then the area S can be computed as ½ times the absolute value of the determinant
Hence, Area = 1/2 det [abs( xB xC )]
___________________[abs( yB yC )]
or for three general vertices, the formula is :
Area = 1/2 det [abs( xA xB xC )]
_____________[abs( yA yB yC )]
_____________[abs( 1 1 1 )]
In addition, there is also a method by using vectors:
The area of triangle ABC can also be expressed in terms of dot products
Area = 1/2{sqr root[(AB.AB)(AC.AC) - (AB.AC)sqr]}
Lastly, there is the Heron's formula :
The shape of the triangle is determined by the lengths of the sides alone. Therefore the area also can be derived from the lengths of the sides.
By Heron's formula:
Area = {sqr root[s(s - a)(s - b)(s - c)]}
where s = ½ (a + b + c) is the semiperimeter, or half of the triangle's perimeter.
Yup these formulas are pretty useful huh =D thats all happy mathematic-ing
acknowledgement : wikipedia
Saturday, June 13, 2009
Hi, im back to post more fun facts about MATHS =)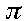
=3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 ... - There are shapes of constant width other than the circle. One can even drill square holes
- In a group of 23 people, at least two have the same birthday with the probability greater than 1/2
- Everything you can do with a ruler and a compass you can do with the compass alone.
- Among all shapes with the same perimeter a has the largest area.
- The next sentence is true but you must not believe it.
- The previous sentence was false
- [ 12+3+4+5+67+8+9=100] There exists at least one other representation of 100 with 9 digits in the right order and math operations in between
- One can cut a pie into 8 pieces with three movements.
- A clock never showing right time might be preferable to the one showing right time twice a day
- Among all shapes with the same area circle has the shortest perimeter.
A. Bogomolny, Did you know that... Random interesting math facts from Interactive Mathematics Miscellany and Puzzles
http://www.cut-the-knot.org/do_you_know/index.shtml, Accessed 14 June 2009
http://www.cut-the-knot.org/do_you_know/index.shtml, Accessed 14 June 2009
Wednesday, June 10, 2009
Hi everyone, this is Seany---
Firstly for today, i came across this really interesting "proving" of an equation and i'll be here to share it with you.
The following is a "proof" that one equals zero.
Consider two non-zero numbers x and y such that
Then x2 = xy.
Subtract the same thing from both sides:
x2 - y2 = xy - y2.
Dividing by (x-y), obtain
x + y = y.
Since x = y, we see that
2 y = y.
Thus 2 = 1, since we started with y nonzero.
Subtracting 1 from both sides,
1 = 0.
This equation seems to be flawless, doesn't it?
--
Also..
Consider the following integral:
INTEGRAL (1/x) dx
Perform integration by parts: let
u = 1/x , dv = dx
du = -1/x2 dx , v = x
Then obtain:
INTEGRAL (1/x) dx = (1/x)*x - INTEGRAL x (-1/x2) dx
= 1 + INTEGRAL (1/x) dx
which implies that 0 = 1.
This also seems flawless right?
--
However, for the first "proving",
The problem with this "proof" is that if x=y, then x-y=0. Notice that halfway through our "proof" we divided by (x-y).
and as for the second one, it is a common mistake in integration by parts. Students often forget about the constant of integration for indefinite integrals. In this case, the constants on both sides will differ by 1.
acknoledgemtns : Su, Francis E., et al. "One Equals Zero!." Mudd Math Fun Facts.
--
have a nice day
Tuesday, June 2, 2009
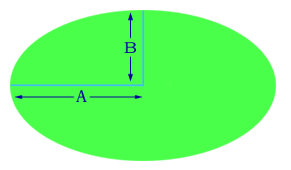As we all know, the area of circle is PiR2.But what about the formula for area of an Ellipse?
Consider the picture shown on the right, where A and B are
semi-major axis of the large and small diameter of the ellipse respectively.
A standard equation for such an ellipse centered at origin:(x2/A2) + (y2/B2) = 1.
The area of ellipse is PiAB , so similar to that of circle!
Facts behind it
The above diagram can be seen as a unit circle that has been stretched by a factor A in the x-direction, and a factor B in the y-direction. Hence the area of the ellipse is just AB times the area of the unit circle.
However, the perimeter of an ellipse is not at all generalize with that of a circle. :)
The area of ellipse is PiAB , so similar to that of circle!
Facts behind it
The above diagram can be seen as a unit circle that has been stretched by a factor A in the x-direction, and a factor B in the y-direction. Hence the area of the ellipse is just AB times the area of the unit circle.
However, the perimeter of an ellipse is not at all generalize with that of a circle. :)
Su, Francis E., et al. "Area of an Ellipse." Mudd Math Fun Facts. .
Xiao Yuting
Wan Tian Chong
